The Nastiest Problem in Finance, Solved?
Einstein: “The measure of intelligence is the ability to change.”
Two or three generations ago, retirement was “easy” as our ancestors worked longer and died younger. Their retirement, if it happened at all, was brief, and for many was covered by a pension and social security. The idea of a thirty-year retirement was not an idea at all; it was unimaginable. If someone did achieve it, they were a statistical anomaly.
Here are some numbers: a 65 year-old American man in 1960 had on average about 13 more years of life. By 1990, that number had increased to 15, and today it is 18, meaning the average man retiring today at 65 makes it to 83. And that is an average. We all know men who retire at 65 and make it past 90. For women, the numbers are even better.
We can credit this situation to science and behavior: better medical care, improved diets, more exercise. But if private enterprise and social security could handle a 10 year retirement, something had to give when retirement stretched into a 20 or 30 year event. The gift of a longer life became the burden of the individual, as companies ditched defined benefit plans and social security could only fund a portion of this elongated retirement. Today’s retirees have to create their own pension income from their assets, and these assets can sometimes fluctuate in value in ways that make us very nervous, as we all experienced during 2020.
This is the challenge to the modern retiree. How do you turn your nest egg, representing the accumulation of a lifetime of work, into a steady source of income, one that will grow over time, avoid excessive risk, outpace inflation, cover your living expenses (with the help of social security), withstand financial shocks, pandemics, and political risk, and still have something left over to leave to your heirs?
William Sharpe, winner of the Nobel Prize in Finance in 1990, has called this decumulation stage of retirement the “nastiest, hardest problem in finance.” This is not exactly reassuring to hear, but despair is not warranted. As we will see, just as you do not need a medical degree to understand that you should eat well, exercise regularly, get proper rest, and take your medications, so you don’t need a PhD in finance to manage your retirement.
What makes this problem so challenging, in Professor Sharpe’s analysis? He looks at the numerous uncertain variables in retirement (how long you will live, what the stock market will deliver during your retirement, future inflation), calculates the thousands of combinations, and tries to optimize the best choice, not only in terms of asset allocation between stocks and bonds, but also in terms of whether to use annuities or not, and, if so, when to annuitize (at the beginning of retirement, middle, or end)? There are thousands of choices. How does an investor make the best one?
First, by introducing annuities into the equation, Professor Sharpe’s analysis does not apply to most retirees. Why not? For the simple reason that most individuals do not want to purchase annuities, despite a theoretical argument for their use, because they dislike the idea of paying a healthy portion of their retirement assets to an insurance company, knowing that when they die, the insurance company gets to keep these assets, not their children or grandchildren (while also introducing counter-party risk because the insurance company must stay solvent for the length of the retirement). For most of us, pooling assets as a way of reducing longevity risk sounds good in theory, until you think through the details.
Second, most investors are not interested in the absolute “best choice.” “Good enough” will do.
Third, we think Professor Sharpe himself would agree there is no perfect solution. Trade-offs are unavoidable. At the risk of putting words into the Professor’s mouth, we think he would respond to the question we posed above by saying, simply: “You can’t.” Your retirement assets are not superheroes; they cannot provide steady income, and grow over time, and avoid taking risk, and outplace inflation, and withstand all financial shocks and political risks, and guarantee something will be left over for your heirs.
What can retirees do to solve this nastiest problem in finance?
The most well-known rule-of-thumb that financial planners use is called the “4% Rule.” This rule says that if you retire at 65 you should withdrawal 4% of your assets in the first year of your retirement, and then increase that amount by the rate of inflation every year after that. For example, if you retire at 65 with $2,000,000, you should withdrawal $80,000 in year 1, and – assuming inflation is 3% – $82,400 in year 2, etc.
Though popular, easy to understand, and simple to implement, the 4% Rule most likely no longer applies to today’s market environment of historically low bond yields and high equity valuations, according to leading financial economists like Wade Pfau. Some financial researchers say that 3% is the new 4%.
If simplicity suits you, the 4% rule can be easily modified. Financial author William Bernstein provided a simple modification in his 2009 book “The Investor’s Manifesto”: “When all is said and done, I still know of no better risk analysis tool for retirees under the age of 70 than this simple narrative: At a 2 percent withdrawal rate, your nest egg will survive all but catastrophic institutional and military collapse: at 3 percent, you are probably safe; at 4 percent, you are taking real chances; and at 5 percent and beyond, you should consider annuitizing most, if not all, of your nest egg.”
Another limitation of the 4% Rule is that it unrealistically assumes that a retiree increases their living expenses at the rate of inflation each year, regardless of what is happening in their lives and in the market. There are no adjustments made to this number in response to strong markets or weak markets, or in response to a change in one’s physical health. The truth is that most retirees adjust their spending over time. They may spend more when the market does well, and cut back when the market does poorly. They may spend more in the early part of their retirement when they are healthy, and less as they age and slow down. Then, as their health deteriorates as they approach the final stage of their life, their spending may increase as health care costs increase. In the 4% rule, the retiree blithely increases their withdrawal by the rate of inflation, year after year, seemingly oblivious to what is going on around them.
Flexibility, or the ability to accept some volatility in your spending from year to year, can be the key to managing one’s assets in retirement. The more ability a retiree has to adjust their spending down in response to a bad market, the better their chances of not outliving their assets, and the greater the percentage amount they can withdrawal earlier in retirement (if you are willing to be flexible in your spending every year, you can probably start off your retirement with a 4% or even 5% withdrawal). Avoiding the regret associated with investing in annuities, or the rigidity of the 4% rule, taking a flexible approach to retirement spending, and revisiting the issue at least once a year, is the most practical strategy for achieving a successful retirement.
In preparing this letter, I found a paper by a mathematics professor entitled: “A Stochastic Control Approach to Defined Contribution Plan Decumulation: ‘The Nastiest, Hardest Problem in Finance’”* The author tackled the problem with equations like this throughout the paper:
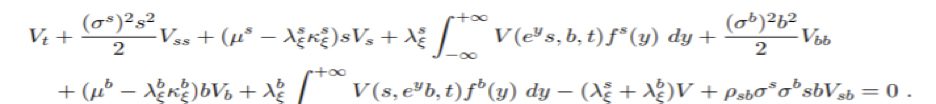
I could take the rest of my life trying to decipher this equation and it would be a complete waste of time. But I was able to understand this footnote in the paper, where the author quotes one of his colleagues who had also studied the retirement problem: “If we have a good year, we take a trip to China,…if we have a bad year, we stay home and play canasta.”
Perhaps this forbidding equation is simply the mathematical expression of this quote. Who knows? Either way, you don’t need to be a Nobel-prize winning economist to manage your retirement assets, nor do you need to be able to do integral calculus. Instead, common sense, flexibility, and vigilance will do.

